Bravais lattice

Clash Royale CLAN TAG#URR8PPP

In geometry and crystallography, a Bravais lattice, named after Auguste Bravais (1850),^[1] is an infinite array of discrete points in three dimensional space generated by a set of discrete translation operations described by:

R=n1a1+n2a2+n3a3displaystyle mathbf R =n_1mathbf a _1+n_2mathbf a _2+n_3mathbf a _3

where n_i are any integers and a_i are known as the primitive vectors which lie in different directions and span the lattice. This discrete set of vectors must be closed under vector addition and subtraction. For any choice of position vector R, the lattice looks exactly the same.

When the discrete points are atoms, ions, or polymer strings of solid matter, the Bravais lattice concept is used to formally define a crystalline arrangement and its (finite) frontiers. A crystal is made up of a periodic arrangement of one or more atoms (the basis) repeated at each lattice point. Consequently, the crystal looks the same when viewed from any equivalent lattice point, namely those separated by the translation of one unit cell (the motif).

Two Bravais lattices are often considered equivalent if they have isomorphic symmetry groups. In this sense, there are 14 possible Bravais lattices in three-dimensional space. The 14 possible symmetry groups of Bravais lattices are 14 of the 230 space groups.

Contents

• 
  1 In 2 dimensions
  


• 
  2 In 3 dimensions
  


• 
  3 In 4 dimensions
  


• 
  4 See also
  


• 
  5 References
  


• 
  6 Further reading
  


• 
  7 External links
  

In 2 dimensions

Further information: Lattice (group)

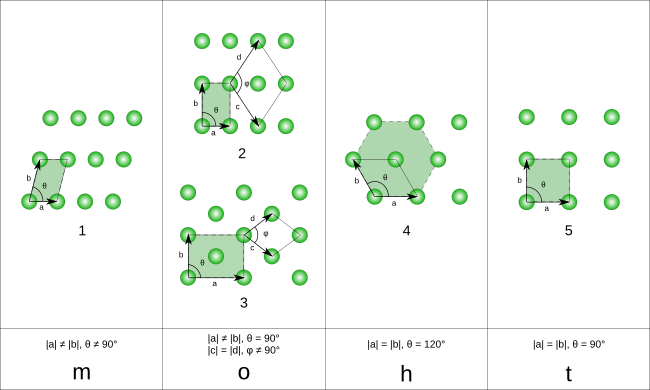
1 – oblique (monoclinic), 2 – rectangular (orthorhombic), 3 – centered rectangular (orthorhombic), 4 – hexagonal, and 5 – square (tetragonal).

In two-dimensional space, there are 5 Bravais lattices,^[2] grouped into four crystal families.

Crystal family	Point group (Schönflies notation)	5 Bravais lattices
		Primitive	Centered
Monoclinic	C2	Oblique
Orthorhombic	D2	Rectangular	Centered rectangular
Hexagonal	D6	Hexagonal
Tetragonal	D4	Square

The unit cells are specified according to the relative lengths of the cell edges (a and b) and the angle between them (θ). The area of the unit cell can be calculated by evaluating the norm ||a × b||, where a and b are the lattice vectors. The properties of the crystal families are given below:

Crystal family	Area	Axial distances (edge lengths)	Axial angle
Monoclinic	absin⁡θdisplaystyle ab,sin theta	a ≠ b	θ ≠ 90°
Orthorhombic	abdisplaystyle ab	a ≠ b	θ = 90°
Hexagonal	32a2displaystyle frac sqrt 32,a^2	a = b	θ = 120°
Tetragonal	a2displaystyle a^2	a = b	θ = 90°

In 3 dimensions

2×2×2 unit cells of a diamond cubic lattice

In three-dimensional space, there are 14 Bravais lattices. These are obtained by combining one of the seven lattice systems with one of the centering types. The centering types identify the locations of the lattice points in the unit cell as follows:

• Primitive (P): lattice points on the cell corners only (sometimes called simple)


• Base-centered (A, B, or C): lattice points on the cell corners with one additional point at the center of each face of one pair of parallel faces of the cell (sometimes called end-centered)


• Body-centered (I): lattice points on the cell corners, with one additional point at the center of the cell


• Face-centered (F): lattice points on the cell corners, with one additional point at the center of each of the faces of the cell

Not all combinations of lattice systems and centering types are needed to describe all of the possible lattices, as it can be shown that several of these are in fact equivalent to each other. For example, the monoclinic I lattice can be described by a monoclinic C lattice by different choice of crystal axes. Similarly, all A- or B-centred lattices can be described either by a C- or P-centering. This reduces the number of combinations to 14 conventional Bravais lattices, shown in the table below.^[3]

Crystal Family	Lattice System	Schönflies	14 Bravais Lattices
			Primitive (P)	Base-centered (C)	Body-centered (I)	Face-centered (F)
Triclinic		Ci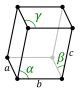
Monoclinic		C2h
Orthorhombic		D2h
Tetragonal		D4h
Hexagonal	Rhombohedral	D3d
	Hexagonal	D6h
Cubic		Oh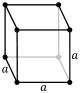

The unit cells are specified according to the relative lengths of the cell edges (a, b, c) and the angles between them (α, β, γ). The volume of the unit cell can be calculated by evaluating the triple product a · (b × c), where a, b, and c are the lattice vectors. The properties of the lattice systems are given below:

Crystal family	Lattice system	Volume	Axial distances (edge lengths)[4]	Axial angles[4]	Corresponding examples
Triclinic		abc1−cos2⁡α−cos2⁡β−cos2⁡γ+2cos⁡αcos⁡βcos⁡γdisplaystyle abcsqrt 1-cos ^2alpha -cos ^2beta -cos ^2gamma +2cos alpha cos beta cos gamma	(All remaining cases)		K2Cr2O7, CuSO4·5H2O, H3BO3
Monoclinic		abcsin⁡βdisplaystyle abc,sin beta	a ≠ c	α = γ = 90°, β ≠ 90°	Monoclinic sulphur, Na2SO4·10H2O, PbCrO3
Orthorhombic		abcdisplaystyle abc	a ≠ b ≠ c	α = β = γ = 90°	Rhombic sulphur, KNO3, BaSO4
Tetragonal		a2cdisplaystyle a^2c	a = b ≠ c	α = β = γ = 90°	White tin, SnO2, TiO2, CaSO4
Hexagonal	Rhombohedral	a31−3cos2⁡α+2cos3⁡αdisplaystyle a^3sqrt 1-3cos ^2alpha +2cos ^3alpha	a = b = c	α = β = γ ≠ 90°	Calcite (CaCO3), cinnabar (HgS)
	Hexagonal	32a2cdisplaystyle frac sqrt 32,a^2c	a = b	α = β = 90°, γ = 120°	Graphite, ZnO, CdS
Cubic		a3displaystyle a^3	a = b = c	α = β = γ = 90°	NaCl, zinc blende, copper metal, KCl, Diamond, Silver

In 4 dimensions

In four dimensions, there are 64 Bravais lattices. Of these, 23 are primitive and 41 are centered. Ten Bravais lattices split into enantiomorphic pairs.^[5]

See also

• Crystal habit


• Crystal system


• Miller index


• Translation operator (quantum mechanics)


• Translational symmetry


• Zone axis

References

1. 
   ^ Aroyo, Mois I.; Müller, Ulrich; Wondratschek, Hans (2006). "Historical Introduction". International Tables for Crystallography. Springer. A1 (1.1): 2–5. doi:10.1107/97809553602060000537. Archived from the original on 2013-07-04. Retrieved 2008-04-21. 
   


2. 
   ^ Kittel, Charles (1996) [1953]. "Chapter 1". Introduction to Solid State Physics (Seventh ed.). New York: John Wiley & Sons. p. 10. ISBN 0-471-11181-3. Retrieved 2008-04-21. 
   


3. 
   ^ Based on the list of conventional cells found in Hahn (2002), p. 744
   


4. 
   ^ ^ab Hahn (2002), p. 758
   


5. 
   ^ Brown, Harold; Bülow, Rolf; Neubüser, Joachim; Wondratschek, Hans; Zassenhaus, Hans (1978), Crystallographic groups of four-dimensional space, New York: Wiley-Interscience [John Wiley & Sons], ISBN 978-0-471-03095-9, MR 0484179 
   

Further reading

• 
  Bravais, A. (1850). "Mémoire sur les systèmes formés par les points distribués régulièrement sur un plan ou dans l'espace" [Memoir on the systems formed by points regularly distributed on a plane or in space]. J. Ecole Polytech. 19: 1–128.  (English: Memoir 1, Crystallographic Society of America, 1949.)


• 
  Hahn, Theo, ed. (2002). International Tables for Crystallography, Volume A: Space Group Symmetry. A (5th ed.). Berlin, New York: Springer-Verlag. doi:10.1107/97809553602060000100. ISBN 978-0-7923-6590-7. 
  

External links

• Catalogue of Lattices (by Nebe and Sloane)


• 
  Smith, Walter Fox (2002). "The Bravais Lattices Song".