Central binomial coefficient

This article includes a list of references, related reading or external links, but its sources remain unclear because it lacks inline citations. Please help to improve this article by introducing more precise citations. (June 2016) (Learn how and when to remove this template message)

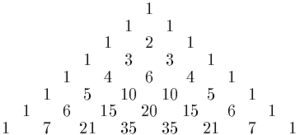
Pascal's triangle, rows 0 through 7. The numbers in the central column are the central binomial coefficients.

In mathematics the nth central binomial coefficient is the particular binomial coefficient

(2nn)=(2n)!(n!)2 for all n≥0.displaystyle 2n choose n=frac (2n)!(n!)^2text for all ngeq 0.

They are called central since they show up exactly in the middle of the even-numbered rows in Pascal's triangle. The first few central binomial coefficients starting at n = 0 are:

1, 2, 6, 20, 70, 252, 924, 3432, 12870, 48620, ...; (sequence A000984 in the OEIS)

Contents

• 
  1 Properties
  


• 
  2 Related sequences
  


• 
  3 References
  


• 
  4 External links
  

Properties

The central binomial coefficients have ordinary generating function

11−4x=1+2x+6x2+20x3+70x4+252x5+⋯displaystyle frac 1sqrt 1-4x=1+2x+6x^2+20x^3+70x^4+252x^5+cdots

and exponential generating function

∑n=0∞(2nn)xnn!=e2xI0(2x),displaystyle sum _n=0^infty binom 2nnfrac x^nn!=e^2xI_0(2x),

where I₀ is a modified Bessel function of the first kind.^[1]

They also satisfy the recurrence

(2(n+1)n+1)=4n+2n+1⋅(2nn).displaystyle binom 2(n+1)n+1=frac 4n+2n+1cdot binom 2nn.

The Wallis product can be written in asymptotic form for the central binomial coefficient:

(2nn)∼4nπn.displaystyle 2n choose nsim frac 4^nsqrt pi n.

The latter can also be easily established by means of Stirling's formula. On the other hand, it can also be used as a means to determine the constant 2πdisplaystyle sqrt 2pi in front of the Stirling formula, by comparison.

Simple bounds that immediately follow from 4n=(1+1)2n=∑k=02n(2nk)displaystyle 4^n=(1+1)^2n=sum _k=0^2nbinom 2nk are

4n2n+1≤(2nn)≤4n for all n≥1displaystyle frac 4^n2n+1leq 2n choose nleq 4^ntext for all ngeq 1

Some better bounds are^[2]

4n4n≤(2nn)≤4n3n+1 for all n≥1displaystyle frac 4^nsqrt 4nleq 2n choose nleq frac 4^nsqrt 3n+1text for all ngeq 1

and, if more accuracy is required,

(2nn)=4nπn(1−cnn) where 19<cn<18displaystyle 2n choose n=frac 4^nsqrt pi nleft(1-frac c_nnright)text where frac 19<c_n<frac 18 for all n≥1.displaystyle ngeq 1.^{[citation needed]}

The only central binomial coefficient that is odd is 1. More specifically, the number of factors of 2 in (2nn)displaystyle binom 2nn is equal to the number of ones in the binary representation of n.^[3]

By the Erdős squarefree conjecture, proven in 1996, no central binomial coefficient with n > 4 is squarefree.

The central binomial coefficient (2nn)displaystyle 2n choose n equals the sum of the squares of the elements in row n of Pascal's triangle.^[1]

Related sequences

The closely related Catalan numbers C_n are given by:

Cn=1n+1(2nn)=(2nn)−(2nn+1) for all n≥0.displaystyle C_n=frac 1n+12n choose n=2n choose n-2n choose n+1text for all ngeq 0.

A slight generalization of central binomial coefficients is to take them as
Γ(2n+1)Γ(n+1)2=1nB(n+1,n)displaystyle frac Gamma (2n+1)Gamma (n+1)^2=frac 1nmathrm B (n+1,n), with appropriate real numbers n, where Γ(x)displaystyle Gamma (x) is the gamma function and B(x,y)displaystyle mathrm B (x,y) is the beta function.

The powers of two that divide the central binomial coefficients are given by Gould's sequence, whose nth element is the number of odd integers in row n of Pascal's triangle.

References

1. 
   ^ ^ab Sloane, N.J.A. (ed.). "Sequence A000984 (Central binomial coefficients)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. 
   


2. 
   ^ Kazarinoff, N.D. Geometric inequalities, New York: Random House, 1961
   


3. 
   ^ Sloane, N.J.A. (ed.). "Sequence A000120". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. 
   

• 
  Koshy, Thomas (2008), Catalan Numbers with Applications, Oxford University Press, ISBN 978-0-19533-454-8 .

External links

• 
  "Central binomial coefficient". PlanetMath. 
  


• 
  "Binomial coefficient". PlanetMath. 
  


• 
  "Pascal's triangle". PlanetMath. 
  


• 
  "Catalan numbers". PlanetMath. 
  

This article incorporates material from Central binomial coefficient on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Clash Royale CLAN TAG#URR8PPP